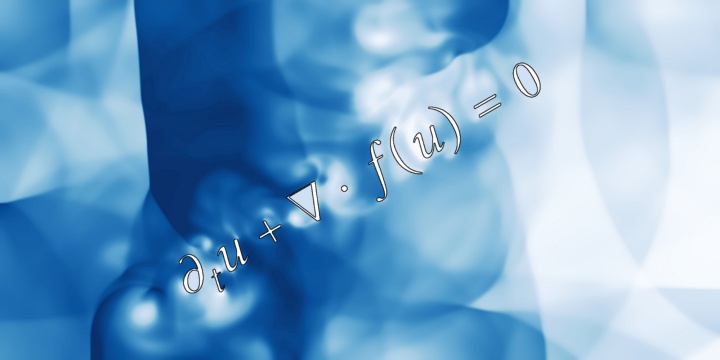Von acht neuen Schwerpunktprogramme (SPP), die der Senat der Deutschen Forschungsgemeinschaft (DFG) in seiner jüngsten Sitzung bewilligte, werden gleich zwei an der Universität Stuttgart eingerichtet: Prof. Mathias Liewald (Institut für Umformtechnik) möchte mit Partnern die etablierte Finite Elemente-Methode zur Auslegung von Umformwerkzeugen und –prozessen um eine datengetriebene Modellierung erweitern. Prof. Christian Rohde (Institut für Angewandte Analysis und numerische Simulation) wird in dem von ihm koordinierten Verbund Hypothesen im Bereich der Strömungsmechanik mathematisch untermauern und eine neue Generation numerischer Simulationswerkzeuge entwickeln.
Prof. Wolfram Ressel, der Rektor der Universität Stuttgart, kommentiert: „Das überproportional gute Abschneiden der Initiativen unserer Universität bei der jüngsten Wettbewerbsrunde um DFG-Schwerpunktprogramme freut uns sehr. Der Erfolg bestätigt die Forschungsstärke, Innovativität und Interdisziplinarität der Profilbereiche Produktionstechnologie und Simulationswissenschaft der Universität Stuttgart wie auch der Stuttgarter Mathematik. Die neuen Schwerpunktprogramme werden diese herausragende Stellung weiter stärken.“
Schwerpunktprogramm „Datengetriebene Prozessmodellierung in der Umformtechnik“, Koordinator Prof. Mathias Liewald
Anlagen und Systeme für die Blech- und Massivumformung müssen effizient und ressourcenschonend produzieren, wenn sie den künftigen Ansprüchen des Standorts Deutschland in punkto Nachhaltigkeit und Wettbewerbsfähigkeit entsprechen sollen. Eine weitere Herausforderung für die Umformtechnik ist der Fachkräftemangel: Dieser macht es schwierig, das für einen erfolgreichen und effizienten Produktionsablauf erforderliche Erfahrungswissen über die prozesssichere Auslegung von Bauteil und Umformsystem auch für die zukünftige Auslegung von robusten und nachhaltigen Prozessen bereitzustellen. Zur Lösung dieser Probleme treiben Forschung und Industrie Entwicklungen zur Digitalisierung von Wertschöpfungsketten derzeit massiv voran.
Gleichzeitig verbesserten sich zuletzt die technischen Voraussetzungen zur Speicherung, Verarbeitung und Analyse großer Datenmengen und damit die Nutzung von realen Produktionsdaten für die Prozessauslegung erheblich. Aufgrund der hohen Kapitalbindung in Umformanlagen und großer wirtschaftlicher Skaleneffekte erscheint die Weiterentwicklung von datengetriebenen Modellen als besonders aussichtsreich, um Wissen zu speichern und die Vorhersagegüte sowie die Erklärbarkeit der Modelle zu erhöhen.
Vor diesem Hintergrund wollen die Forschenden im SPP „Datengetriebene Prozessmodellierung in der Umformtechnik“ neue Methoden des Data-Science mit den Ergebnissen aus der etablierten Finite Elemente-Methode (FEM) zur Auslegung von Umformwerkzeugen und -prozessen sowie mit Domänenwissen verknüpfen und dabei die interdisziplinären Forschungsgebiete Umformtechnik, Automation und Data-Science integrieren. Dem Programmausschuss gehören demgemäß auch Prof. Marco Huber vom Institut der Industrielle Fertigung und Fabrikbetrieb der Universität Stuttgart sowie Kolleg*innen der TUM München und der Universität Kiel an. Die Forschenden wollen die FEM-Auslegung um eine datengetriebene Modellierung erweitern, damit zukünftig auch nichtlineare Phänomene bei der Prozessauslegung effizient und erklärbar berücksichtigt werden können. Dies soll Prognosen zur Qualität von Bauteilen im Vergleich zum heutigen Stand erkennbar steigern.
Schwerpunktprogramm „Hyperbolische Erhaltungssätze in der Fluidmechanik: Komplexität, Skalen, Rauschen (CoScaRa)“, Koordinator Prof. Christian Rohde
Ein Überschallknall, wie er im März über Stuttgart zu hören war, entsteht durch Stoßwellen in komprimierbaren Strömungen. Möchte man diesen Effekt oder auch andere Transportprozesse in den Natur- und Ingenieurwissenschaften mathematisch modellieren, erfordert dies oft Systeme von hyperbolischen partiellen Differentialgleichungen wie etwa die aus der Strömungsmechanik bekannten Eulergleichungen. Allgemeiner bilden hyperbolische Modelle die Grundlage numerischer Simulationen und darauf basierender Entscheidungen in vielen gesellschaftlich relevanten Fragen.
Dazu gehören zum Beispiel das computerbasierte Design von Luft- und Raumfahrzeugen, die Wettervorhersage oder Aspekte der Klimaforschung. Trotz der fundamentalen Bedeutung dieser mathematischen Modelle in der Strömungsmechanik sind viele Grundlagenfragen zu hyperbolischen Gleichungen bis heute völlig offen.
Vor diesem Hintergrund möchten Forscher*innen aus den Bereichen der Mathematik, der Strömungsmechanik und der theoretischen Physik im SPP „Hyperbolische Erhaltungssätze in der Fluidmechanik: Komplexität, Skalen, Rauschen (CoScaRa)" völlig neue Ansätze zu hyperbolischen Gleichungssystemen angehen. Beteiligt sind neben der Universität Stuttgart bisher die Universitäten Mainz und Leipzig, die TU Darmstadt sowie die RWTH Aachen.
Möglich werden diese bisher nicht für möglich gehaltene Ansätze durch neue Resultate aus der theoretischen Mathematik und Entdeckungen aus der Strömungsmechanik, die insbesondere zum Verständnis der Interaktion von turbulenten Strömungsregimen und Stoßwellen beitragen können. Konkret geht es dabei um die aus der Geometrie entlehnte Idee wilder Lösungen (Komplexität), um moderne Konzepte der Mehrskalenmodellierung (Skalen) und bahnbrechende stochastische Modellierungstechniken (Rauschen).
Als visionäres Ziel sollen bisher nur weitgehend phänomenologisch belegte Vermutungen zur Entwicklung und Verteilung der kinetischen Energie in turbulenten Strömungen wie die Kolmogorovhypothese mathematisch untermauert werden. Dies würde auch zu einer neuen Generation von numerischen Simulationswerkzeugen führen, auf die der Exzellenzcluster „Datenintegrierte Simulationswissenschaft“ (EXC 2075, Simtech) an der Universität Stuttgart abzielt.
Fachlicher Kontakt:
Prof. Dr. Mathias Liewald, Universität Stuttgart, Institut für Umformtechnik, Tel. +49 711 685 83840, E-Mail
Prof. Dr. Christian Rohde, Universität Stuttgart, Institut für Angewandte Analysis und numerische Simulation, Tel. +49 711 685 65524, E-Mail