Zwischen den Gebäuden der Elektrotechnik (mit den vorgelagerten Hörsälen) und der Universitätsbibliothek liegt eine höhergelegte und durch ein Pflasterraster strukturierte Rasenfläche.
Die Kante dieser erhöhten Fläche hat eine sehr zackige Form: Sie wurde von den Architekten der Lernstraße als „Blitzweg“ gestaltet.
Dieser Blitz zielt von der Elektrotechnik auf das Hochhaus, in dem die Institute der Physik beheimatet sind.
Blitze sind ein aus Gewittern vertrautes Naturphänomen, welches mit großen Gefahren verbunden ist: Blitzschlag kann für Menschen tödlich enden oder Brände auslösen. Blitze entstehen in Gewitterwolken, in denen sehr hohe elektrische Spannungen vorliegen. Bei derartigen Hochspannungen kann es in Luft, die an sich ein schlechter elektrischer Leiter ist, zu elektrischen Durchschlägen kommen, bei denen sehr starke elektrische Ströme durch schmale „Kanäle“ fließen:
Wir nehmen das als Blitz wahr.
Die Möglichkeit ähnlicher Durchschläge und elektrischer Entladungen muss immer berücksichtigt werden, wenn man technische Einrichtungen plant, die mit Hochspannung (mehr als 1000 Volt) arbeiten.
Dementsprechend besteht das Warnzeichen für Hochspannungseinrichtungen aus einem stilisierten Blitz.
🧒 Balanciere entlang des Blitzes, und bestimme seine Länge, indem du Schritte zählst.
Vergleiche mit der Länge eines Zickzack-Wegs entlang der Pflastersteine im Hochbeet.
Physikalischer Hintergrund
Was ist eigentlich ein Blitz und warum ist er gezackt?
Das helle Leuchten eines Blitzes entsteht dadurch, dass durch den etwa zentimeter-dicken sogenannten Blitzkanal ein extrem starker elektrischer Strom fließt, der die Luft auf Temperaturen von einigen zehntausend Grad erhitzt, sodass aus der Luft ein leuchtendes Plasma wird – wie es auch in der Sonne oder in einer Kerzenflamme vorkommt.
Bevor es dazu kommt, laufen typischerweise eine Reihe verschiedener Prozesse ab:
In der Gewitterwolke findet durch Kollisionen zwischen Eiskristallen und Wassertropfen eine Ladungstrennung statt. Die nach oben steigenden Eiskristalle führen zu einer elektrisch positiv geladenen Oberseite der Gewitterwolke, während die Unterseite der Wolke negativ aufgeladen wird.
Die elektrischen Spannungen zwischen Wolke und Erdboden können dann Millionen Volt betragen, aber trotzdem findet zunächst kein elektrischer Durchschlag statt, weil normale Luft ein guter elektrischer Isolator ist. Stattdessen findet von der Wolke aus in Richtung Erdboden eine Abfolge von Vorentladungen statt, die jeweils eine ca. 50 m lange Strecke durch die Luft ionisieren, wodurch diese elektrisch leitfähig wird. Diese Entladungen des sogenannte Leitblitzes schließen an die jeweils vorherige an, können sich aber in ihrer Richtung ändern – was im Endeffekt die gezackte Form des Blitzes bewirkt.
Wenn der Leitblitz den Erdboden erreicht und somit der gut leitfähige Blitzkanal zwischen Wolke und Erdboden gebildet ist, beginnt die eigentliche Blitzentladung. Für den Bruchteil einer Sekunde fließen extrem starke elektrische Ströme, die das Gas im Blitzkanal zu einem Plasma erhitzen und das helle Aufleuchten verursachen. Meist folgen mehrere derartige Entladungen schnell nacheinander durch denselben Blitzkanal, wodurch der Blitzschein flackert. Durch die sehr hohen Temperaturen dehnt sich das Gas im Blitzkanal schlagartig aus, was zu einer Druckwelle führt, die wir als Donner wahrnehmen.
Blitze sind also ein Naturphänomen mit anspruchsvollen, auch von aktueller Forschung nicht vollständig erklärten physikalischen Ursachen. Gleichzeitig spielen sie in der Hochspannungstechnik eine wichtige Rolle. Somit ist es naheliegend, dass die Verbindung zwischen den Gebäuden der Fachbereiche für Physik bzw. für Elektotechnik innerhalb der Lernstraße der „Blitzweg“ ist.
Mathematischer Hintergrund
Die Manhattan-Metrik
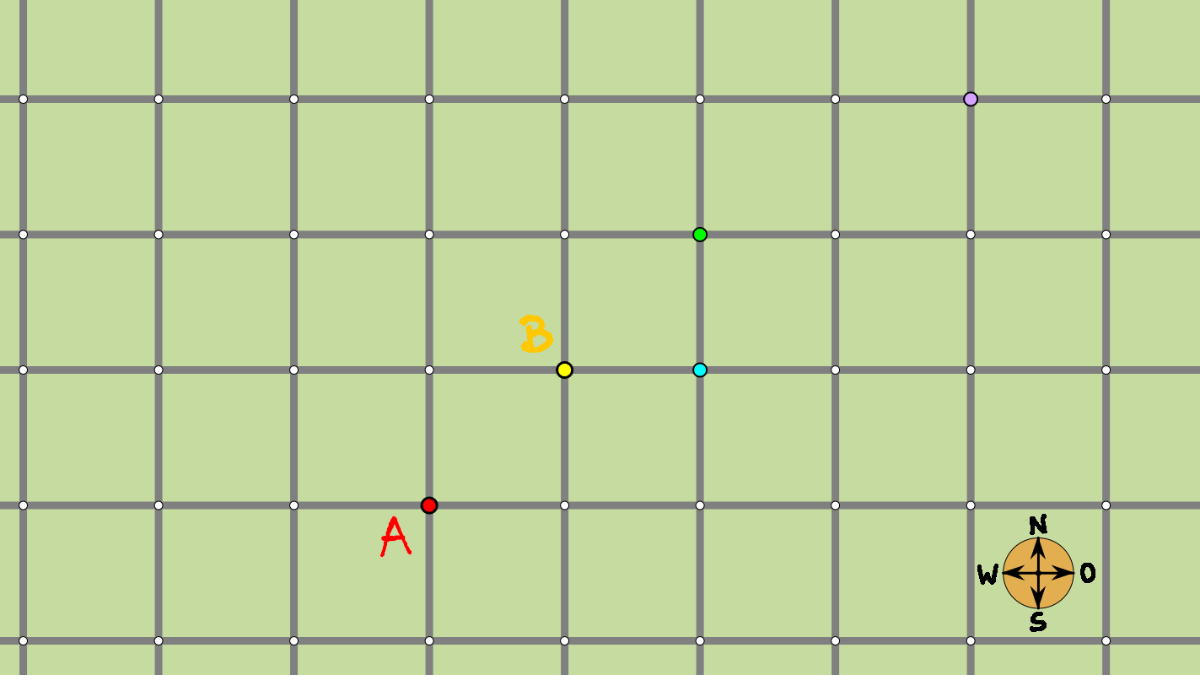
In der Rasenfläche verlaufen Pflasterstreifen, die diese strukturieren. Diese Streifen bilden ein kariertes Gitter aus Pfaden, das wir uns (nach Art echter Mathematiker und Mathematikerinnen) unendlich weit fortgesetzt denken — wir ignorieren also den gezackten Rand.
Diese Pfade verlaufen (grob) in nord-südlicher bzw. ost-westlicher Richtung.
Wenn man von einer Kreuzung des Gitters zu einer anderen gehen will, hat man die Auswahl zwischen verschiedenen Möglichkeiten:
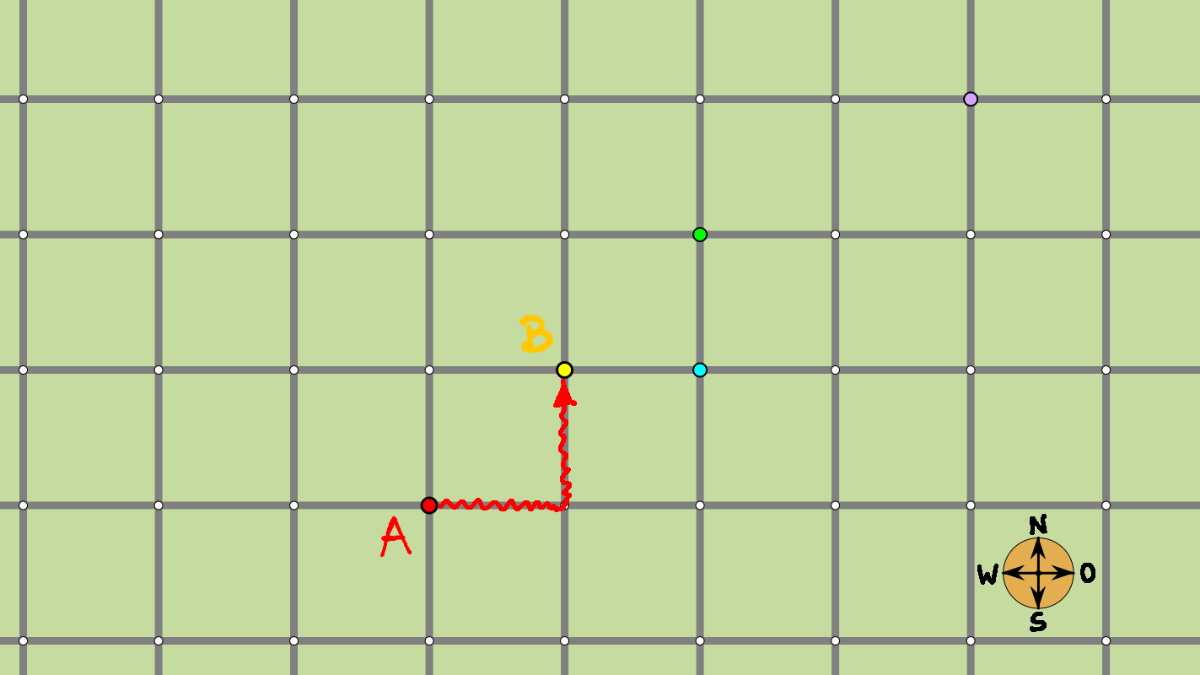
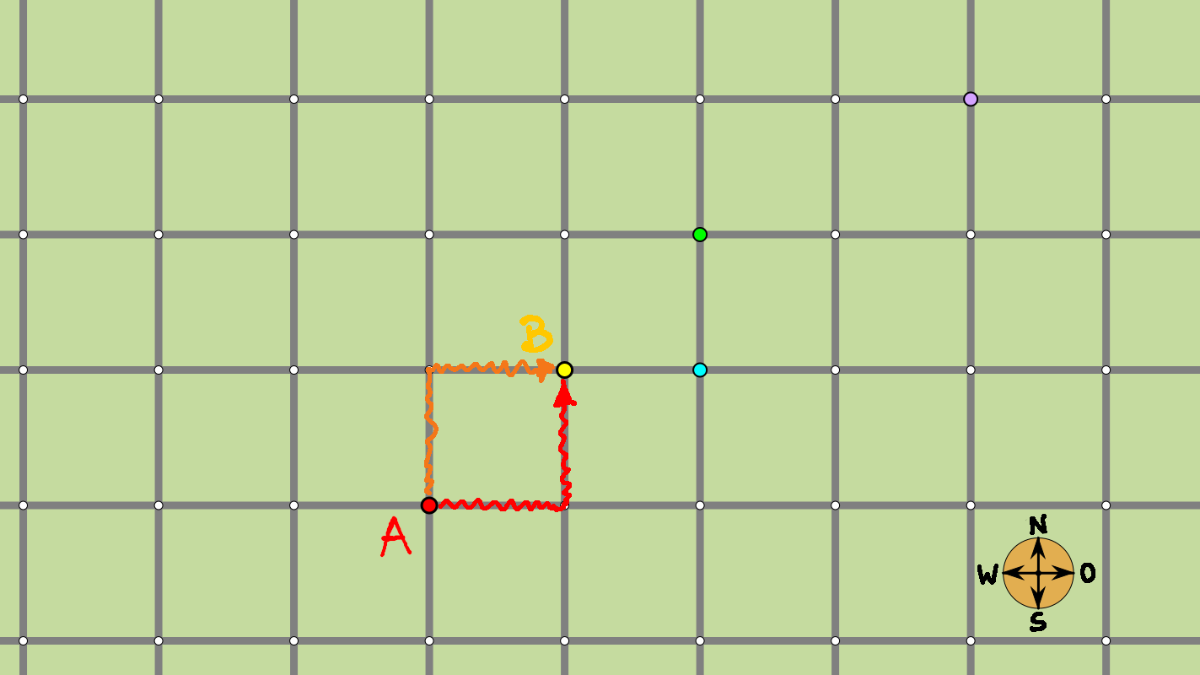
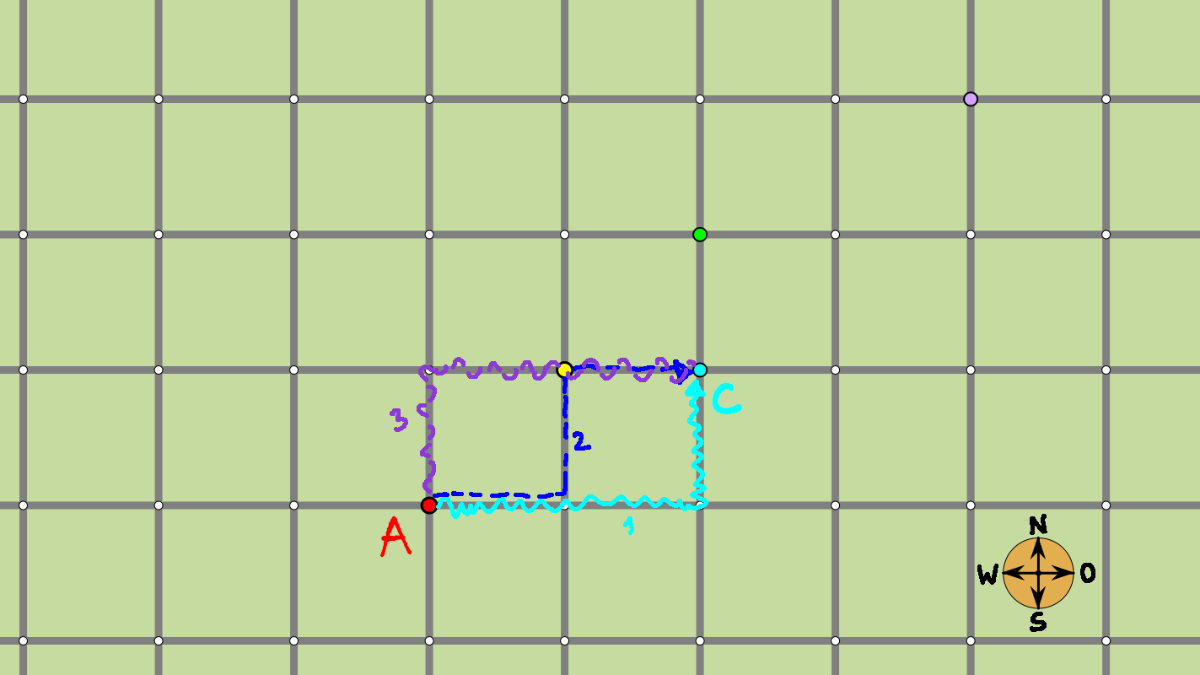
Um entlang der Pfade von A nach B zu gelangen, kann man zum Beispiel zuerst nach Osten, dann nach Norden gehen oder zuerst nach Norden und dann nach Osten abbiegen.
Beide Wege sind gleich lang!
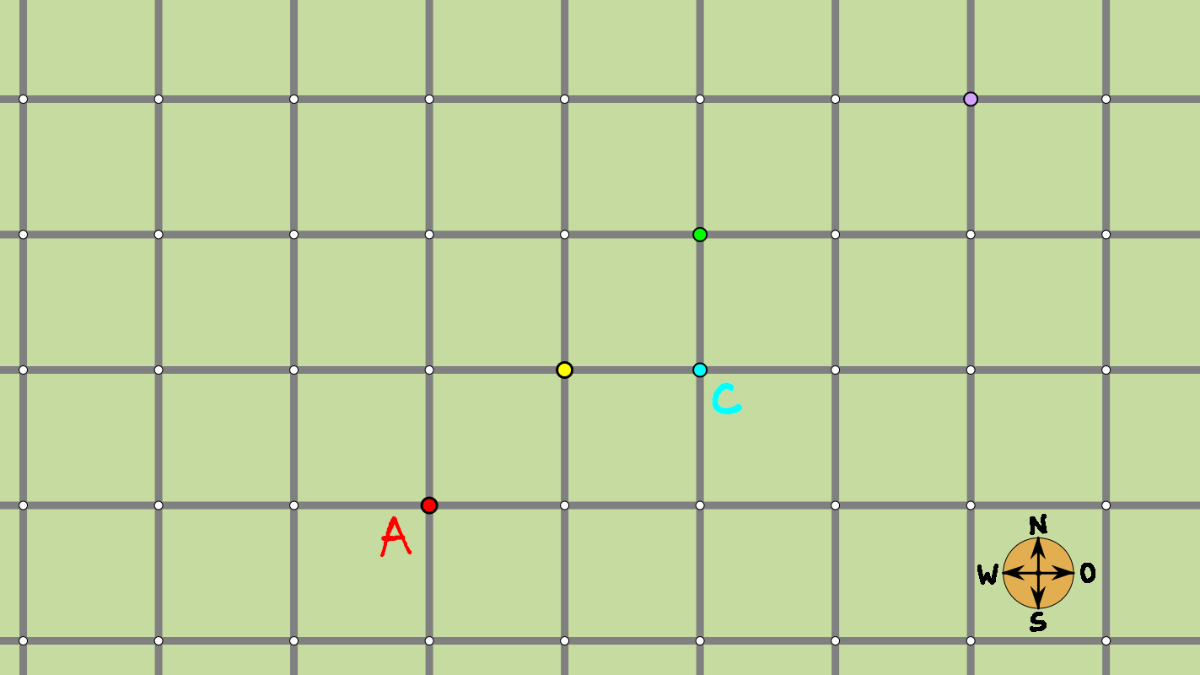
Von A nach C gibt es drei Wege, die alle die gleiche (kürzest mögliche) Länge haben;
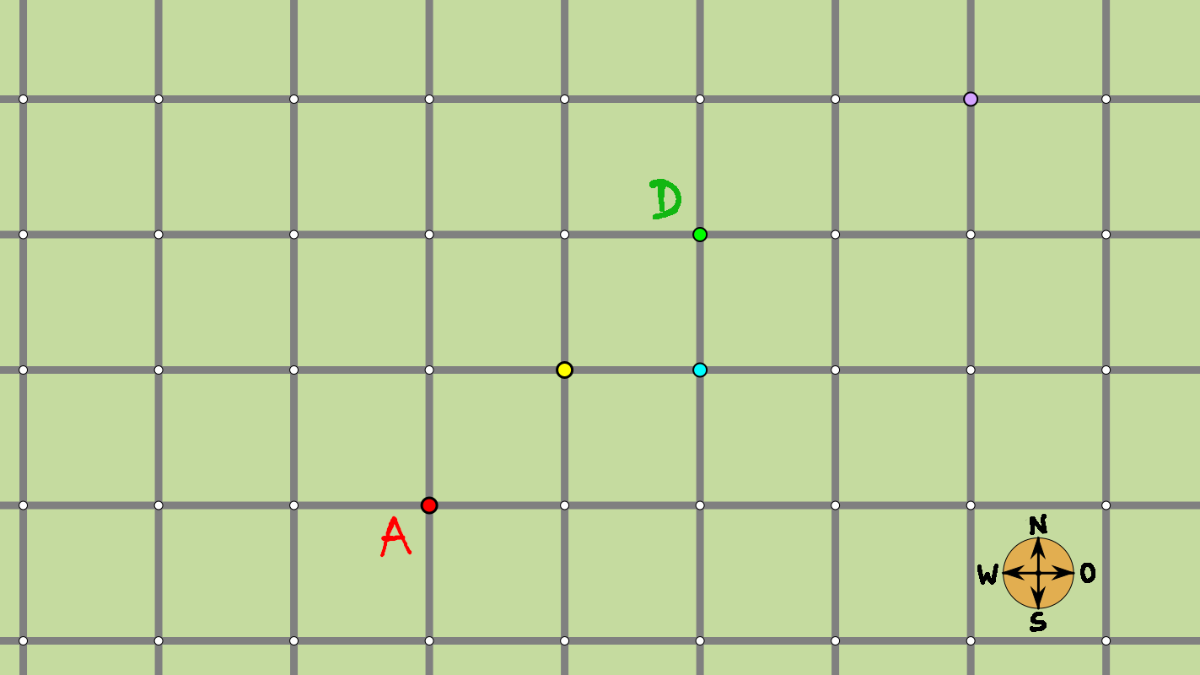
von A nach D schon 6 (alle mit Länge 4), und
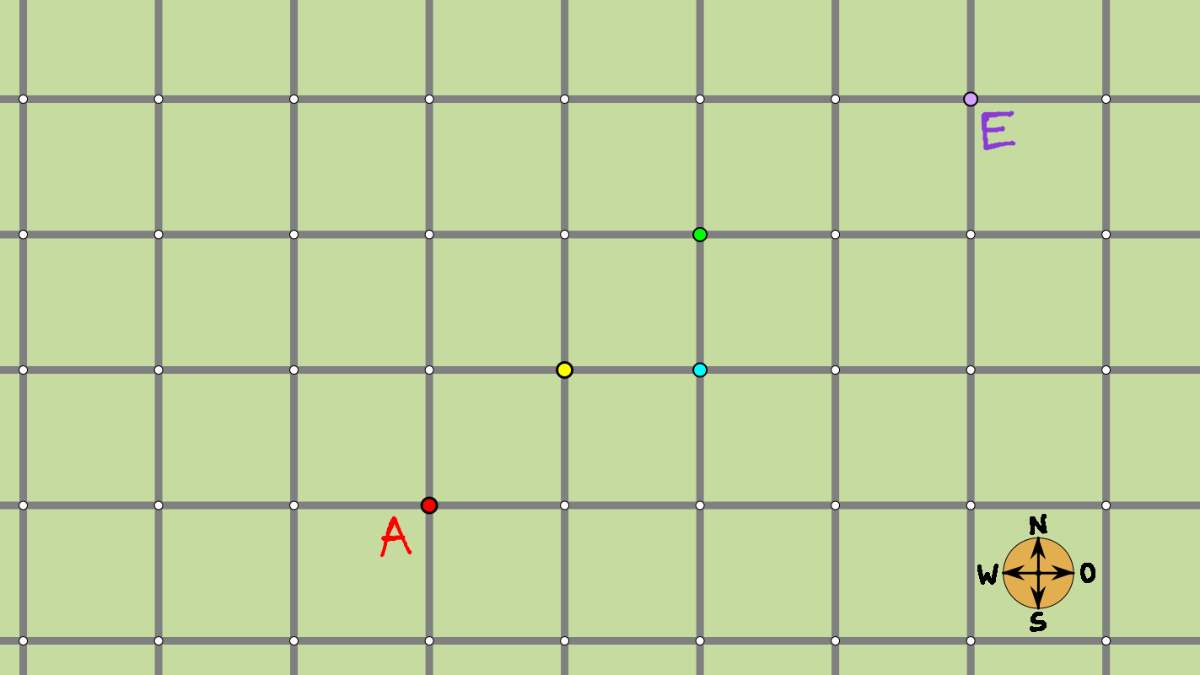
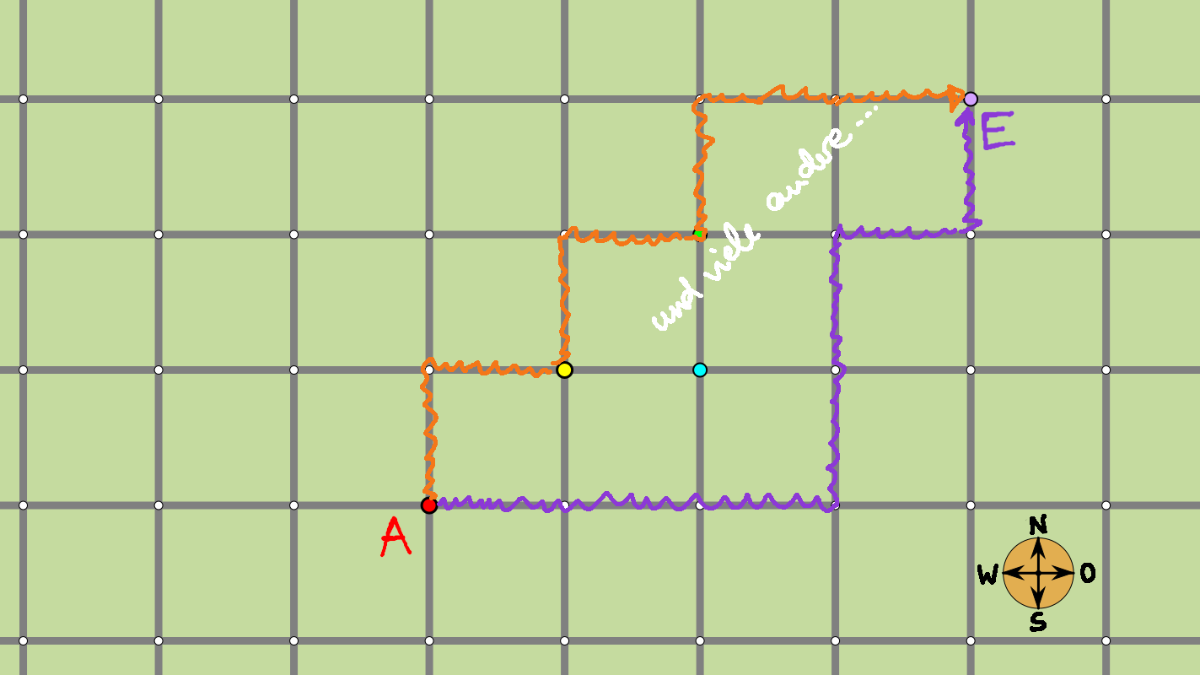
von A nach E sogar 35 verschiedene Wege der Länge 7.
Eine rekursive Formel
Allgemein kann man die Anzahl der kürzesten Wege zwischen zwei Punkten A und X rekursiv bestimmen:
Wir bezeichnen mit s die Zahl der Karos, die man in Ost-West-Richtung überwinden muss, um von A nach X zu kommen, mit t die benötigte Anzahl solcher Schritte in Nord-Süd-Richtung.
Dann ist (in einer Längeneinheit, die der Kantenlänge eines Karos entspricht) s+t die Länge eines kürzesten Wegs von A nach X. Wir schreiben W(s,t) für die Anzahl aller kürzesten Wege.
Dann gilt für alle Zahlen s,t :
W(s,t) = W(t,s),
W(s,0) = 1,
und W(s,t) = W(s-1,t) + W(s,t-1) wenn s und t beide größer als Null sind.
Insbesondere ergibt sich W(s,1) = s+1 für jede Zahl s.
Damit lassen sich (mit s=1=t für X=B, mit s=2, t=1 für X=C, und s=2=t für X=D) die oben behaupteten Anzahlen kürzester Wege schnell bestimmen: Es gilt W(1,1) = 1+1 = 2, W(2,1) = 2+1 = 3, und W(2,2) = W(2-1,2)+W(2,2-1) = 2W(2,1) = 2⋅3 = 6.
Für den Abstand von A nach E können wir die rekursive Formel mehrfach benutzen:
W(4,3) = W(4-1,3) + W(4,3-1) = W(3,3) + W(4,2)
= W(3-1,3) + W(3,3-1) + W(4-1,2) + W(4,2-1) = 3W(3,2)+W(4,1) = 3(W(3-1,2)+W(3,2-1))+(4+1) = 3(W(2,2)+W(3,1))+5
= 3(6+4)+5 = 35.
Binomial-Koeffizienten
Mit der eben bestimmten rekursiven Formel kann man zeigen, dass die Anzahl W(s,t) mit dem Binomialkoeffizient s+t über s
übereinstimmt: Man kann also die Anzahl W(s,t) aus dem Pascalschen Dreieck herauslesen.
Üblicherweise lernt man die Binomialkoeffizienten im Kontext der kombinatorischen Wahrscheinlichkeitsrechnung kennen: Dort verwendet man, dass s+t über s
die Anzahl der Möglichkeiten angibt, aus s+t vielen Elementen genau s viele auszuwählen. Hier bei uns findet sich das wieder als Anzahl der Möglichkeiten, aus s+t durchlaufenen Kreuzungen genau s mal in Ost-West-Richtung weiter zu gehen.
Es ist durchaus sinnvoll, den Abstand zwischen den Kreuzungen so zu messen, dass man die Länge einer kürzesten Verbindungen entlang der Pflasterung bestimmt.
Es gibt auf der Rasenfläche (für Leute, die sich an die gepflasterten Wege halten) im Allgemeinen aber mehrere kürzeste Verbindungen zwischen zwei Kreuzungen.
Dieser Abstandsbegriff ist in der Mathematik unter der Bezeichnung Manhattan taxicab metric
bekannt, weil die Straßen in Manhattan solch ein Karomuster bilden: Für einen Taxifahrer dort gibt es auch oft mehrere Möglichkeiten, auf kürzestem Weg (entlang der Straßen) von einer Kreuzung zur anderen zu kommen.
Wer die lange Reise scheut, kann auch in den Innenstädten von Mannheim oder Tuttlingen solche Straßenraster finden.
