Vor dem Haupteingang zum Gebäude Pfaffenwaldring 9 sind die Leerstühle aus Beton platziert:
Das Wortspiel Leerstuhl — Lehrstuhl
erinnert an die Ordinarien, also die ordentlichen Professoren
oder eben Lehrstuhlinhaber
.
Die Leerstühle werden durch eine Darstellung als Parallelprojektion wieder aufgegriffen im Mosaik vor dem Haupteingang zum Gebäude Pfaffenwaldring 7.
🧒 Wie viele Leute können sich nebeneinander auf die verschieden breiten Leerstühle setzen?
... und
wie viele Kuscheltiere?
In der Entstehungszeit der Plastik (Mitte der 70er Jahre) waren sicher die Proteste der 68er Studentenbewegung präsent, die sich auch gegen abgehobene Professoren, deren scheinbar allmächtige Position und steil ansteigende Hierarchien richteten:
Unter den Talaren — der Muff von tausend Jahren
Die machtvoll und autoritär besetzten Positionen sind geräumt ... die Plätze in der Sonne werden gerne von Studierenden genutzt.
Gar so breit wären die Sitzflächen selbst für den gewichtigsten Professor aber nicht nötig - vielleicht darf man hier auch Bänke oder Sitzreihen erkennen, gestaffelt wie im Hörsaal.
Die Leerstühle erinnern auch an leere Reihen in den Hörsälen während der Pandemie ...
Mathematik?
Grundsätzlich kann man zu jeder endlichen Abfolge von Zahlen ein Bildungsprinzip
als Formel angeben, mit deren Hilfe sich diese ersten Glieder aus ihrer jeweiligen Nummer ergeben — sogar viele verschiedene Formeln …
die Vorhersage
birgt dann eine gewisse Willkür.
(Nichtsdestotrotz sind die Natur- und Ingenieurwissenschaften voll von Beispielen, bei denen solche auf den ersten Blick willkürlich in die Daten hinein interpretierten Muster zu brauchbaren Theorien geführt haben.)
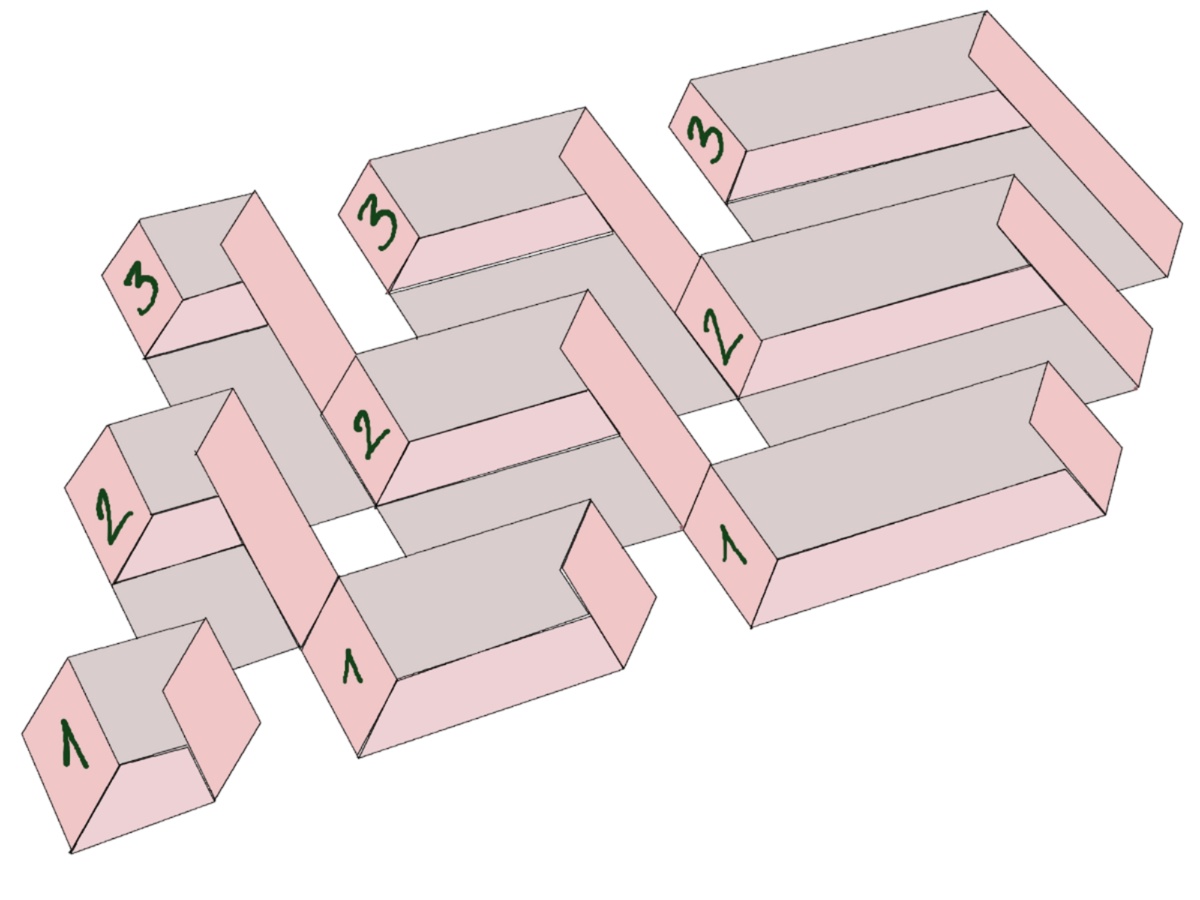
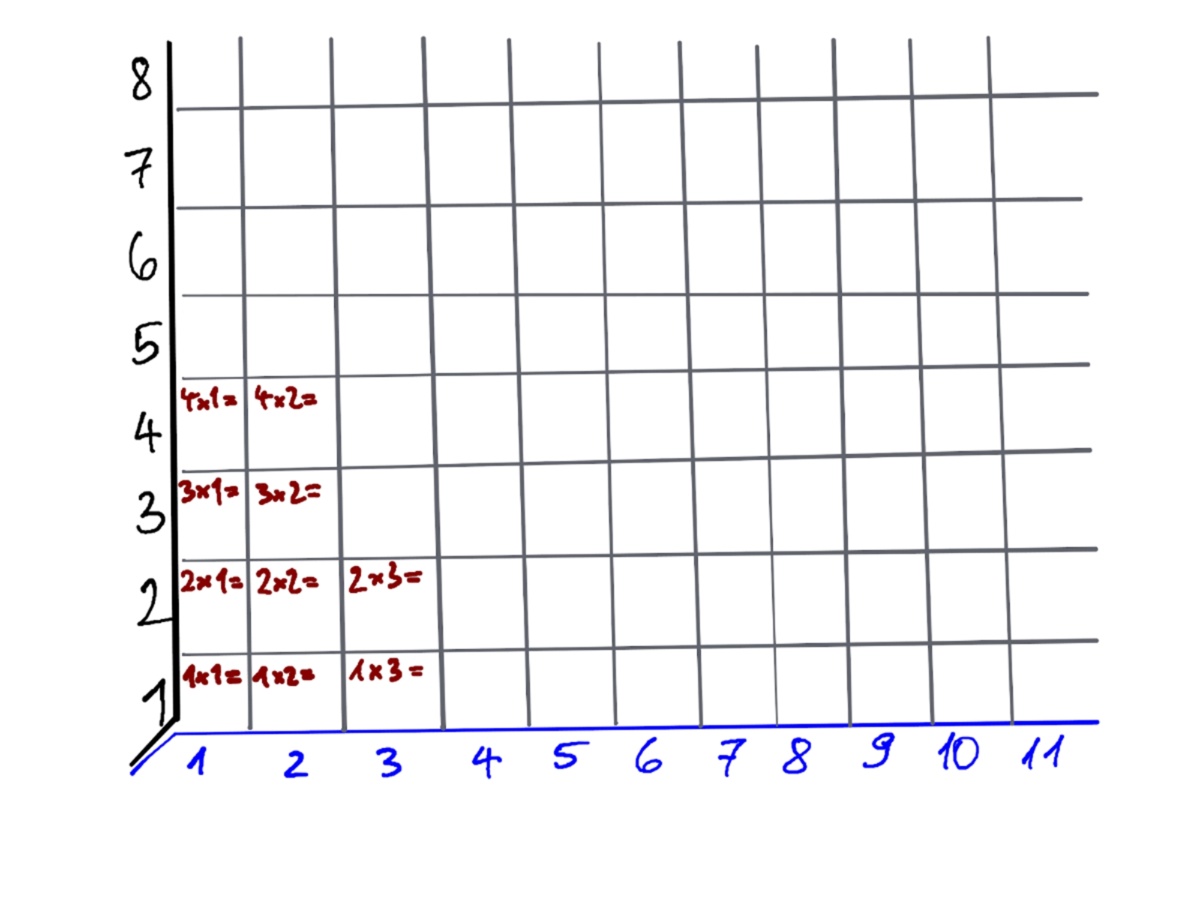
Wir wollen in die Zahlen, die wir aus Höhe und Breite der Leerstühle lesen, eine Anordnung, ein Bildungsprinzip und dann eine Fortsetzung konstruieren.
Die Bildfolge versucht das Bildungsprinzip und seine Fortsetzung zu veranschaulichen.
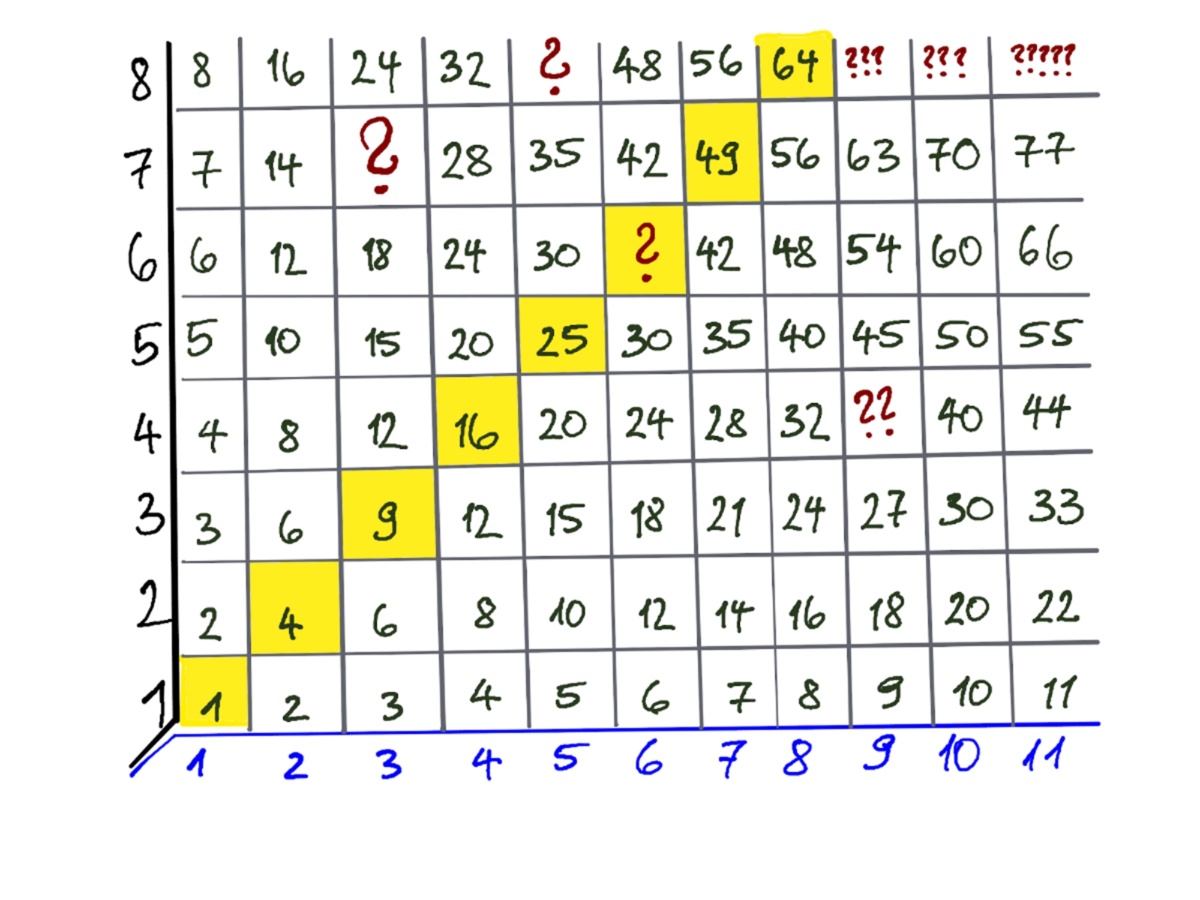
🧒 Wer mag, kann die fehlenden Einträge in den mit Fragezeichen gekennzeichneten Feldern ergänzen.
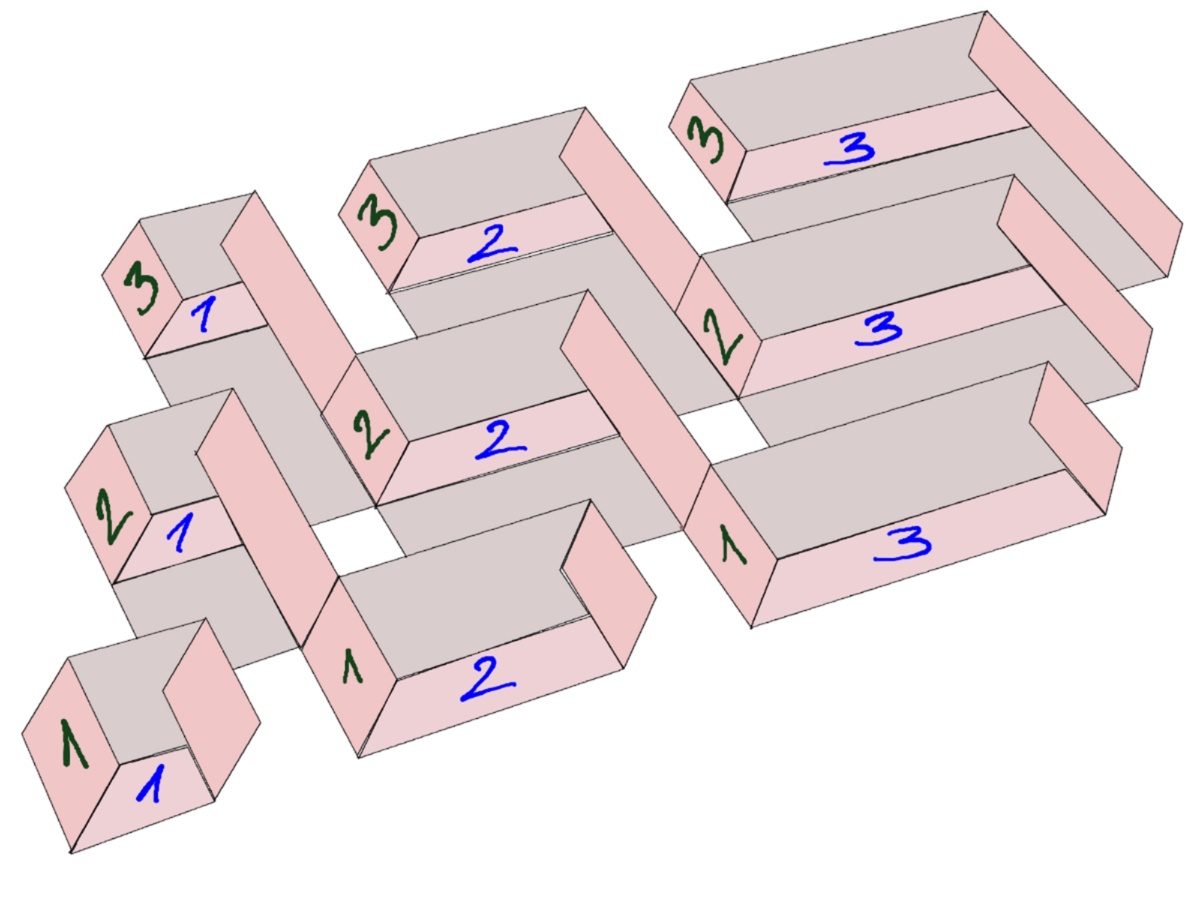
In der ersten Reihe ändert sich die Breite des Sitzmöbels von links nach rechts zunehmend.
Mit jeder Reihe, die wir weiter nach hinten gehen, ändert sich analog die Höhe.
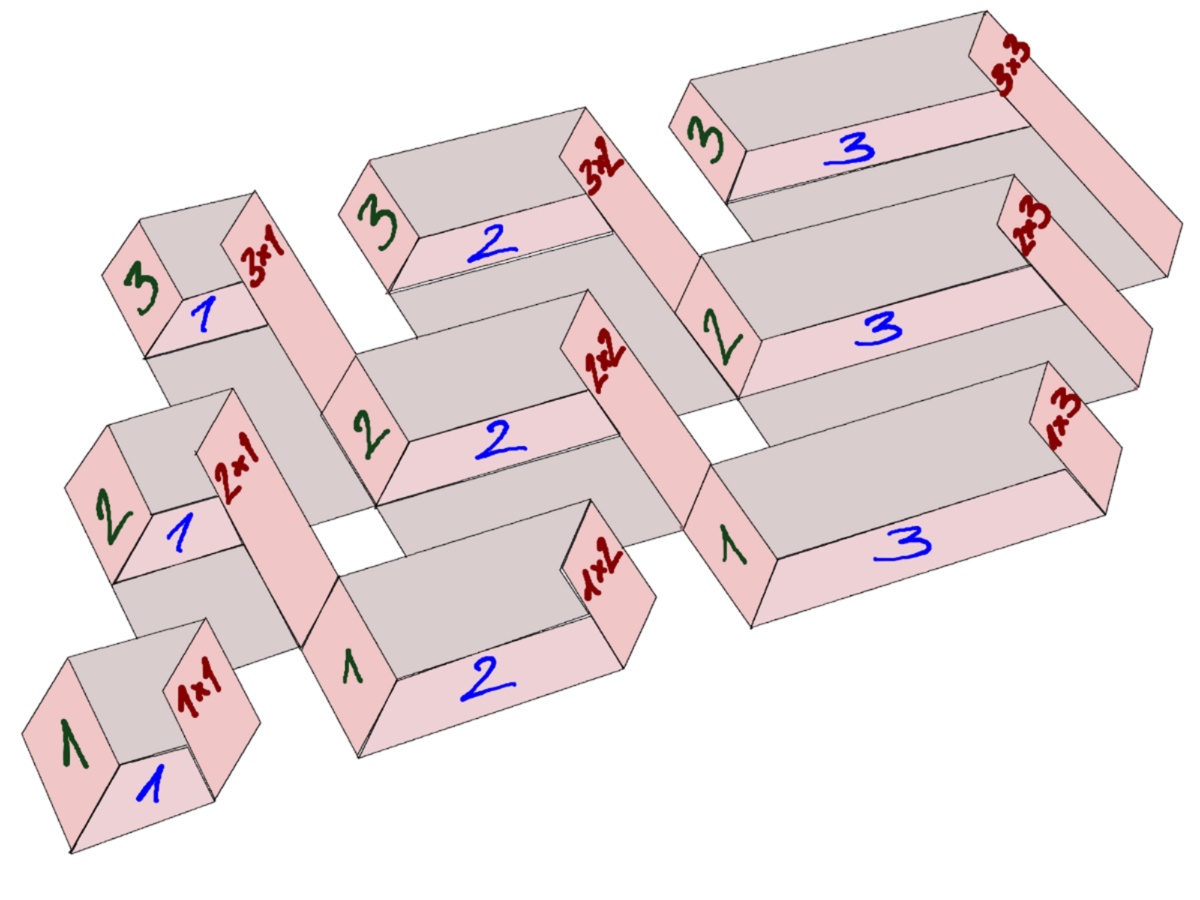
Da die Tiefe immer konstant bleibt, ergibt sich die Maßzahl des Volumens jedes Sitzmöbels aus dem Produkt Höhe mal Breite.
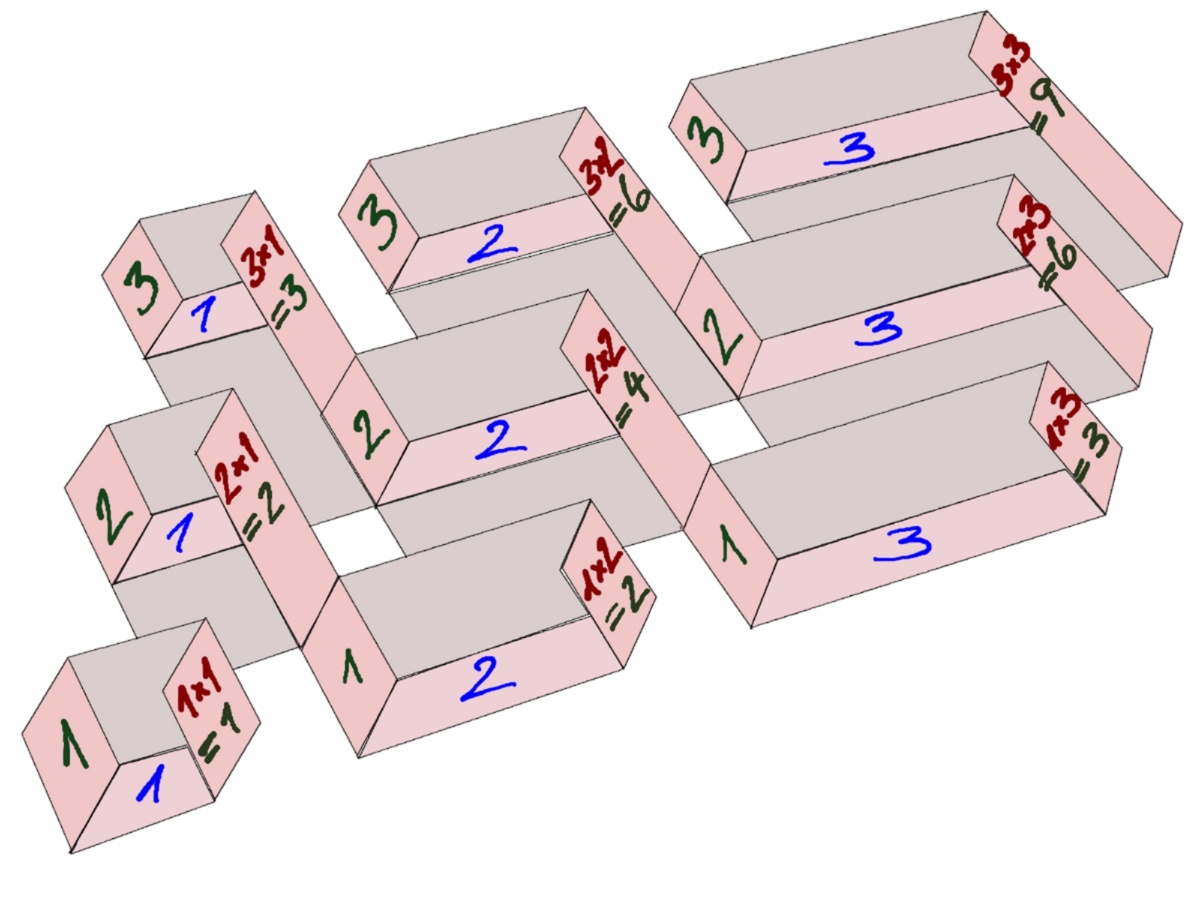
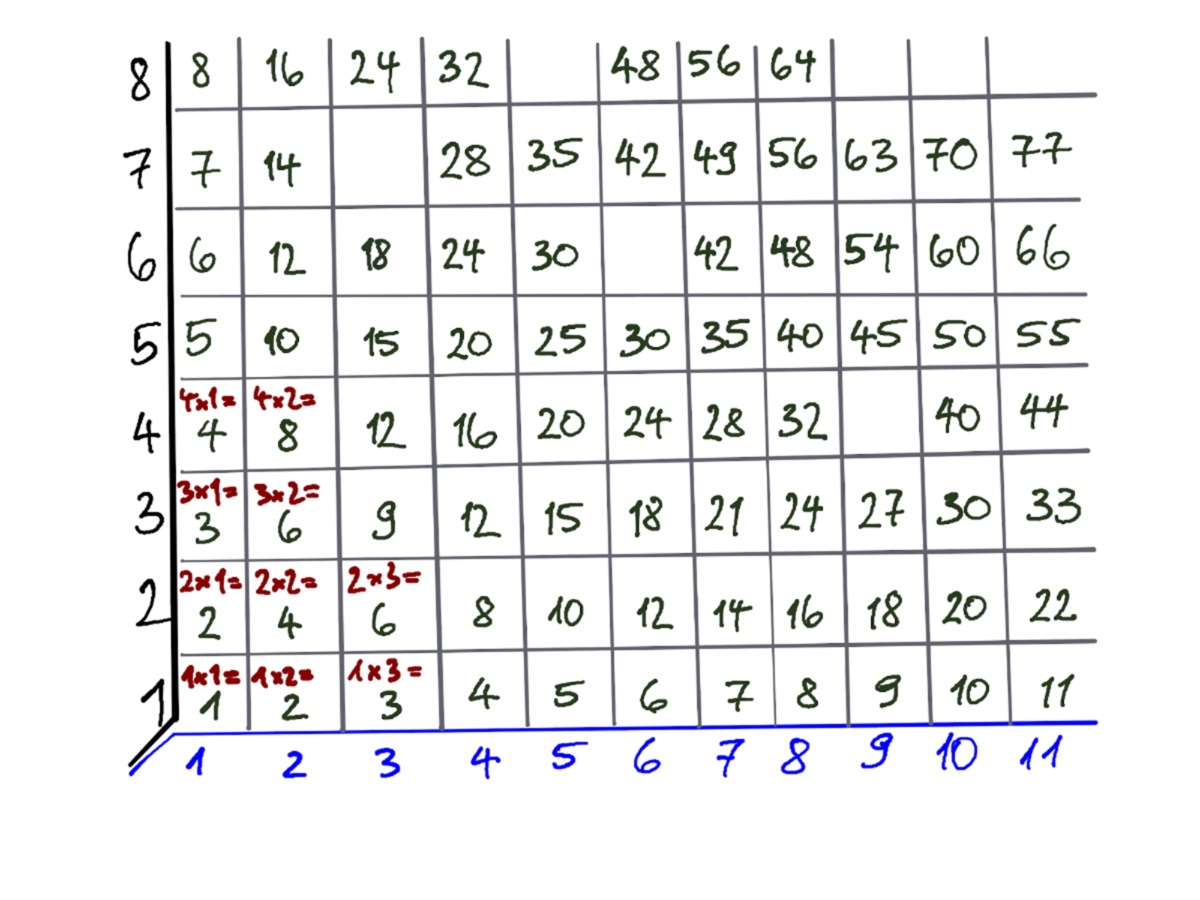
Das Bildungsprinzip Multiplikation
führt auf eine Tabelle, deren Symmetrie eine fundamentale Rechenregel aufzeigt:
Die Kommutativität der Multiplikation x⋅y=y⋅x.
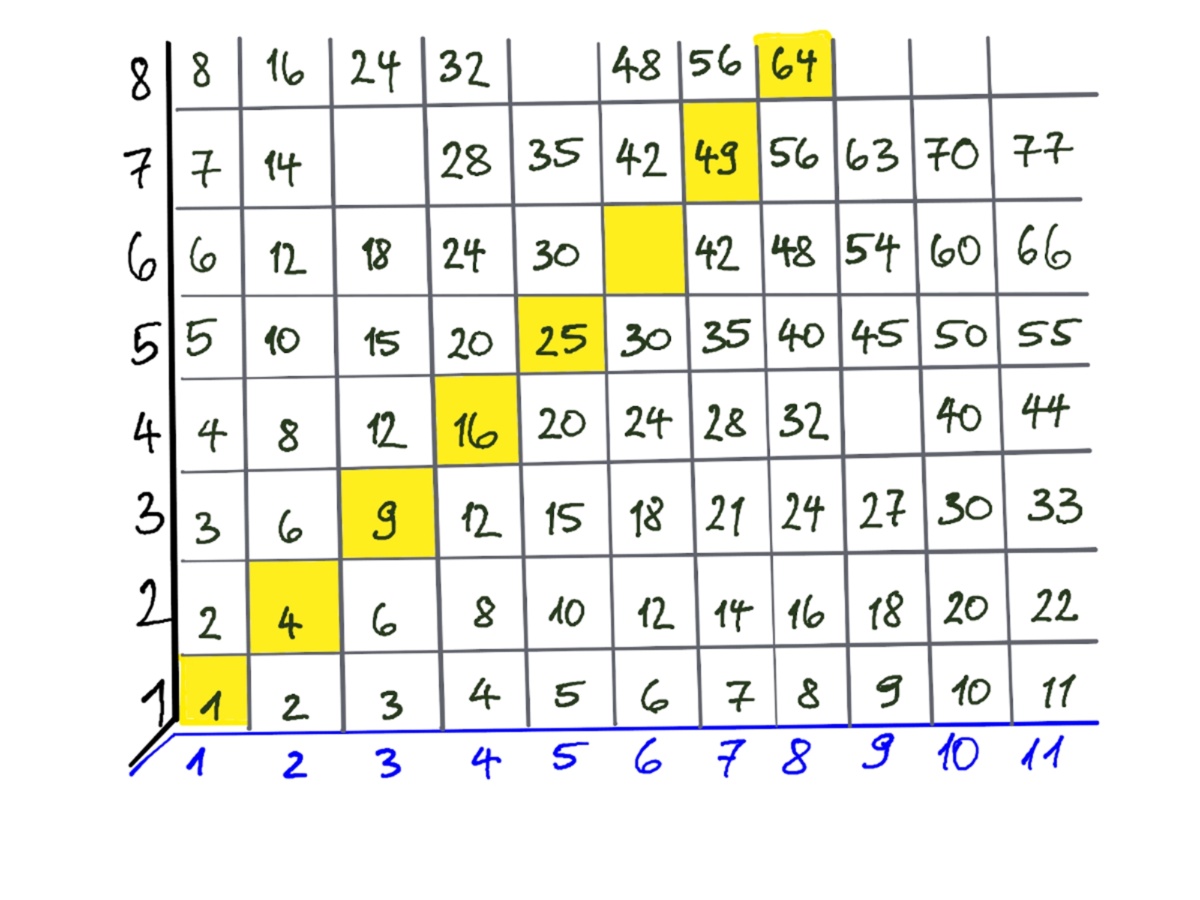
Außerdem findet man auf der Diagonalen der Tabelle die Quadratzahlen.