Die Raumkurven 3. Ordnung entstehen als Schnitt zweier Flächen 2. Ordnung (Quadriken) unter Abspaltung einer Geraden. Sämtliche Quadriken, die eine gegebene Raumkurve 3. Ordnung enthalten, bilden ein zweiparametriges Quadrikenbüschel, aufgespannt von drei Quadriken.
|
|
 |
 |
 |
Kubische Parabel
Die Normalform der kubischen Parabel ist gegeben durch
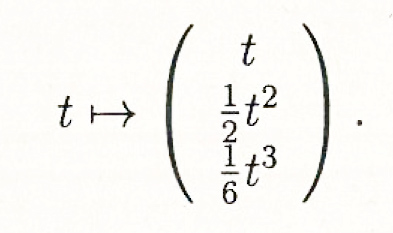
Das Quadrikenbüschel wird aufgespannt von z. B. einem parabolischen Zylinder, einem Kegel und einem Paraboloid.
Kubische hyperbolische Parabel
Die Normalform der kubischen hyperbolischen Parabel ist gegeben durch
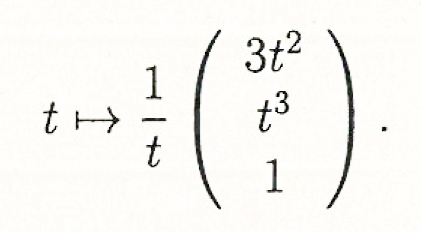
Das Quadrikenbüschel wird aufgespannt von z.B. einem parabolischen Zylinder, einem hyperbolischen Zylinder und einem hyperbolischen Paraboloid.
Kubische Ellipse und kubische Hyperbel
Die Normalform der kubischen Ellipse, bzw. der kubische Hyperbel ist gegeben durch
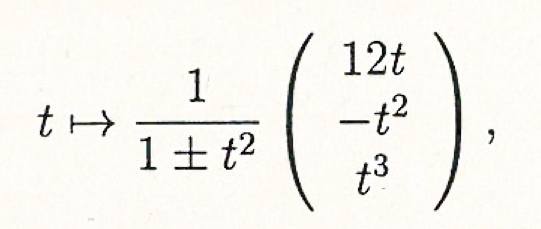
Wobei sich das "+" auf die kubische Ellipse und das "-" auf die kubische Hyperbel bezieht. Das Quadrikenbüschel wird im Fall der kubischen Ellipse aufgespannt von z.B. einem elliptischen Zylinder, einem Kegel und einem Paraboloid, im Fall der kubischen Hyperbel von z.B. einem hyperbolischen Zylinder, einem Kegel und einem Paraboloid.
Ein Spezialfall ist der kubische Kreis. Er spiel eine Roll ein der physiologischen Optik als Ort der einfach gesehenen Punkte einer festen Augenstellung (Horopter). Er ist auch der Ort der Lotfußpunkte von einem gegebenen Punkt auf der Erzeugenden eines hyperbolischen Paraboloids.
Bemerkung
Die Raumkurven 1. Ordnung sind die Geraden, die Raumkurven 2. Ordnung die Kegelschnitte. Der allgemeine Schnitt zweier Quadriken führt zur Raumkurve 4. Ordnung, z.B. die Viviani-Fenster.
Literatur
K. Fladt und A. Baur. Analytische Geometrie spezieller Flächen und Raumkurven. Vieweg Braunschweig 1975




