Singularität
Längs einer Raumkurve p(t) im R3 bewegt sich der Kurvenpunkt p(t) mit seiner Tangente g(t) und seiner Schmiegebene e(t) (beide seien orientiert). Eine Kurvenstelle p(t0) heißt singulär, wenn mindestens eines dieser Kurvenelemente dort stationär ist (d.h. eine entsprechende Ableitung nach t verschwindet). An einer singulären Kurvenstelle können Punkt, Tangente und Schmiegebene ihre Bewegungsrichtung jeweils beibehalten oder umkehren (Rückkehrelement).
Mögliche Fälle
Es können kein, ein, zwei oder drei Kurvenelemente Rückkehrelemente sein, d.h. es gibt
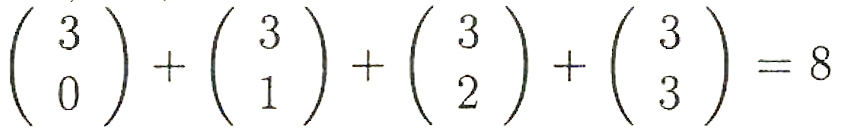
verschiedene Typen singulärer Kurvenstellen.
Der Punkt, die Tangente und die Schmiegebene können eigentlich oder uneigentlich (d.h. Fernelemente) sein. Dies ergibt die vier Möglichkeiten (wobei „e“ für eigentlich und „u“ für uneigentlich steht).
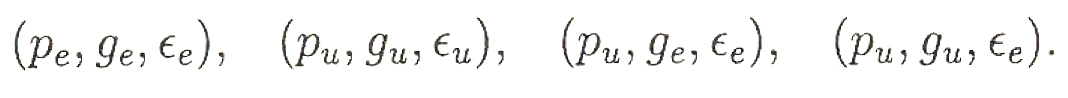
Es lassen sich also insgesamt 4 x 8 = 32 verschiedene Kurvenstellungen bezüglich ihrer Singularität und ihrer Eigentlichkeit untersuchen.
Darstellung
Die gewählten rationalen Kurven niedrigster Ordnung (nach H. Wiener) werden als Hüllkurven einer Folge von Tangenten (blau gespannte Fäden) dargestellt, so dass die Kurvenpunkte als Schnittpunkte, die Schmiegebene als Aufspannebene je zweier benachbarter Tangenten erscheint.
Jede der Raumkurven (mit Ausnahme der beiden singuläritätsfreien Modelle 1.1 und 2.1) zeigen genau zwei zueinander duale Singularitäten (dabei bedeutet „r“, dass das jeweilige Element ein Rückkehrelement ist):

Bei der ersten Teilserie liegt die erste Kurvenstelle in der Würfelmitte des Modells, ihre Tangente und Schmiegebene parallel zu einer Kante bzw. einer Seitenfläche des Würfels. Die zweite Kurvenstelle ist uneigentlich.
Bei der zweiten Teilserie verlaufen die geraden Asymptoten a (grün) und die zu ihnen senkrecht gestellten asymptotischen Schmiegebene y der zweiten Kurvenstelle parallel zu einer Kante bzw. einer Seitenfläche des Würfels. a ∩ a ist die Würfelmitte. Die gerade Asymptote der ersten Kurvenstelle und eine asymptotische ebene Parabel p (zweiter oder höherer Ordnung) sind eingefügt. p ist die Schnittkurve der eigentlichen Schmiegebene der zweiten Kurvenstelle mit derjenigen Zylinderfläche, die die gesamte Raumkurve als Leitkurve und die erste Kurvenstelle als Fernpunkt der Erzeugenden hat.



